RK Software Solutions

ABN 99155402085

Parramatta NSW 2150

Australia

(all RKALC web applications are intellectual property of RK Software Solutions, replicating the apps in any way may be persecuted by law)

The Strut and Tie Calculator

About RKALC

RKALC is a program meant to be a companion for structural engineers during their daily routine, akin to a programmable calculator. It's loaded with numerous solutions all accumulated over the years, like those golden days reference books, like the Reynolds Handbook or the Steel Designers Manual, presented in a more efficient and modern way! The RKALC project targets senior and principal engineers who need to verify the work of others. It is also for entry-level individuals who have just started their careers and are eager to keep up with the pressure without needing to wait for supervision. It allows engineers to verify and check their own work produced by other methods, namely, sophisticated, and trendy software packages that could be misused, like driving a Ferrari the very next day of obtaining a license. RKALC aims to be reliable and trustworthy, clear, and transparent. We have put the Australian Standard in the heart of the RKALC code, as well as the local construction and design dialects, while keeping an eye on the international standards (in particular, Eurocode and ACI) to compare the outcomes and make more sense of them. This is particularly relevant when formulae are shared between our code and an international one. As of August 2022, you should find over 25 apps in one Windows user interface. This number will keep increasing to cover most of the concrete, steel, masonry, and loading standards.

The Strut and Tie Method

STM is a very efficient and simple way to represent the stress flow within concrete element, or parts of it that are under the D region category, where Bernoulli assumptions are not appliable. Some say that the use of this method goes back to early 20^th century, yes, some 120 years ago, when concrete was a new thing, and engineers used to rely on their intuition and expectation of load path.

STM was given several boosts between sixties and early eighties, when Schlaich et. al published guidance on the theory and given typical example with load paths. Later, international codes started to implement and -regulate it if you wish, to keep up with engineers, who always challenge the status quo.

In recent decades, computers have developed astronomically, to an extent that simulation of cracked concrete and non-linear analysis are becoming a standard, more interestingly the load path is now easy to find via Topology Optimisation software packages, yet STM remains indispensable despite being lower bound type.

Typically, you would start with certain model, or triangulated load path, and assume truss as well as node depths, then draw geometry and analyse to check the stresses and reinforcement. This cycle keeps repeating until reaching reasonable convergence, i.e., stresses are slightly above code limits to claim the maximum truss for minimum REO percentage.

Clearly it is tiring and needs to be automated somehow, hence the RKALC's STM calculator.

General rules to follow:

1. The concrete structure is basically divided into either B (Bernoulli) regions where the beam theory applies and stress distribution is linear within the section, or D (Disturbed) regions where it doesn't.

2. Within the D regions, truss analogy can be applied by following the load path lines (principal stresses) and representing them as straight struts (compression members - concrete) and ties (tension members - reinforcement) intersect in nodes (concrete)

3. The angle between diagonal Struts and horizontal line is feasible between 25º and 65º

4. Equilibrium must be maintained while developing the STM model, and concrete must not fail before the steel reinforcement yields

5. Tension is neglected in concrete, and forces in struts are uniaxial

6. Anchorage and detailing are essential

7. There is no exact STM model; however, there are poor and good models.

8. Struts can be categorized into prism, bottle, and fan

9. Nodes (concrete) are categorized into 4 types: CCC, CCT, CTT, TTT (C stands for compression, and T stands for tension):

10. Stresses within struts, ties, support and under load regions must be within allowable code limits.

STM Wall

As in all of RKLAC apps, the left box is to receive the user's inputs related to material properties, geometry, and loads.

Worked Example 1 - Pile Cap

Let us take the following example, taken from Lonnie Pack's book titled -Australian Guidebook for Structural Engineers, with simplifications as in Figure 2

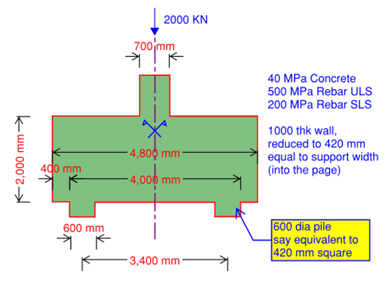
Conservatively, if we take wall depth of 1865mm (say the column load is applied 135 mm below the top of the wall and insert the numbers in STM Calculator, we get the following geometry and analysis results

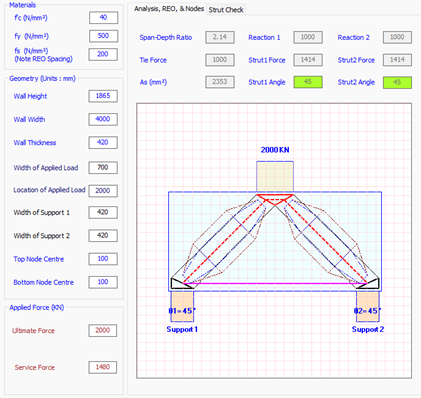
With a tie force of 1000 KN, required reinforcement is 2352 mm, say we provide 6N24 which is not very bad.

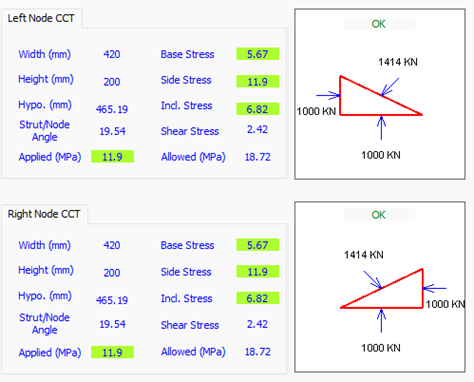
Now we check the bottom nodes, at left and right, in Figure 4, here you will see the geometry of each node, and applied stresses, including shears resulting from strut force being not normal to node, and combined stresses using double Mohr circle.

With AS3600-2018, the CCT node capacity is (f=0.65) x (b=0.8) x 0.9 x (f'c=40) = 18.72 MPa.

Top node is split into 2 nodes, left and right, with load distribution at the top similar to the truss reactions at the top, we have symmetry, see Figure 5

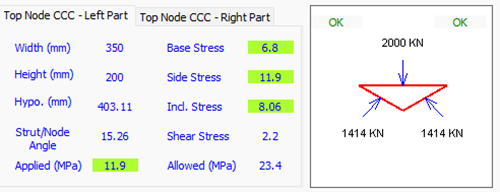
In general cases, if the wall is not symmetric, top node should look like Figure 6, i.e. RKALC is able to articulate this in no time:

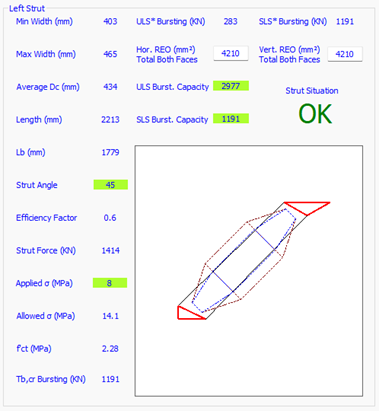
Once all of the node are passing and reinforcement is good, then click on -Strut Check tab, to verify bursting capacity / bursting reo where applicable (we have bottle shaped struts here)

See Figure 7, here RKALC calculates the tension capacity of concrete, and checks both service and ULS cases. Look at the bottle shapes, the thin one represents ULS case, and wide is for SLS.

The app starts with finding the geometry of each bottle, and average width DC specified in the AS 3600-2018, then checks the stresses, and limit states in the play. In this very example Tb,cr or the concrete capacity at tension / bursting is 1191 KN, smaller than applied strut load of 1414, hence bursting reo is required.

For 45 angle, horizontal and vertical reo are the same (you can always change the reo distribution and the software will update).

Once the software says OK for everything, then the user should proceed in marking up the design after checking anchorage of the reinforcement past the critical section of the node (see AS3600-2018 and ACI for guidance)

Worked Example 2 - Shear Wall on Columns

Let us look at this case in , whereby a shear wall is landing on two columns. Something we commonly see when there is no room to take the wall all the way down due to space constrains.

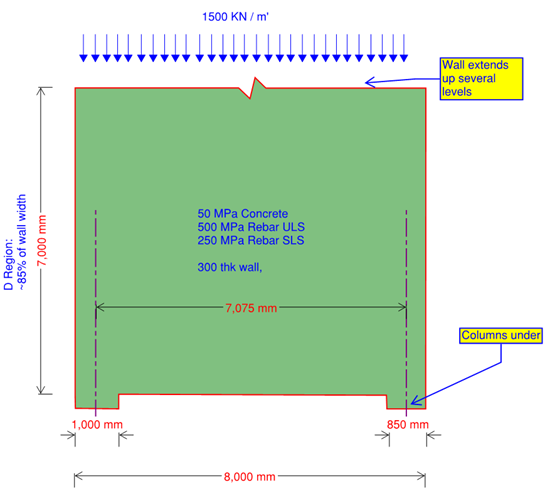
Such a wall would be taking several load scenarios, gravity and lateral.

In this example we will be addressing uniform loading coming from gravity, and note that the wall will suffer uniform stress flow from this case at upper levels until it lands onto the supporting columns.

Typically, the D region would start from the bottom to around 85% of the wall breadth. You can actually see this in FEA models, but be careful, DO NOT design the wall using stress / elastic method, it is simply wrong and not applicable, here you should take the wall to STM Calculator.

Complementary non-linear analysis would help the designer benchmark the percentage at which she/he is utilising the wall. We are talking about circa 10 to 15% margin. or maybe more, if you are having extra degrees of indeterminacy in the play, examples include having thick slabs under, or continuity in the wall. Heavy reinforcement at the first 2 levels is something can be also participating, and needless to mention the concrete properties. Read section 2 of AS3600 for non-linear analysis and criteria to pass these NLFEA.

For walls like this be mindful that the main reinforcement should be lumped at the bottom, and distributed at around 10 to 15% of the D region's depth. Make sure that anchorage is well checked and boundary elements are provided on both edges (closed ties) to confine the stressed zones very well.

The struts we are having here are fan type, where many references do not require bursting check per se, nevertheless, RKALC keeps checking this and gives the freedom to the designer to take it or leave it. We strongly recommend the user to keep an eye on bursting check at all times regardless of the strut type.

See for the user input and graphical representation of the wall, we have chosen a bottom node depth of 800 ( 2 x 400 mm), and widen the top node to extend over the wall breadth. Reinforcement required here is 3281 mm², some 6N28 distributed in two layers should suffice.

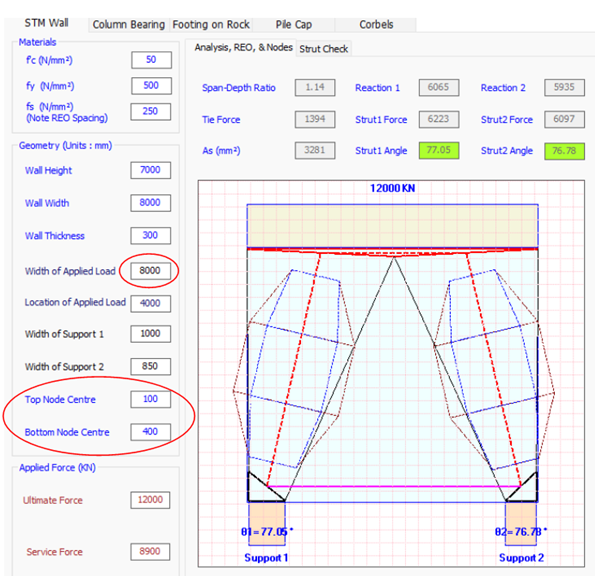
Ensure to have the reinforcement developed correctly and be centred around the node depth to avoid stress concentration, look at for how to calculate the length available and for providing standard hooks to reduce the demand on full anchorage requirements. See AS3600 for this and ACI 318 M for more guidance.

You might be having, under extreme conditions, high yield reinforcement (macalloy or equivalent), in these case you must provide anchor plates and provide local bursting reinforcement.

In this very case, we recommend a screenshot from the software and scale it in pdf software (like Bluebeam), and measure the worst possible anchorage provided.

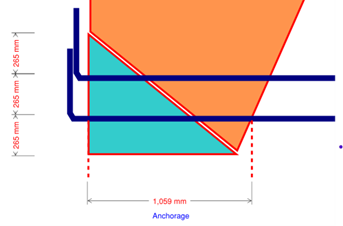
Naturally, node checks come, look at following figure

Worked Example 3 - Foundation on Rock

Foundations on rock is a very special topic for engineers to grasp, in particular for Sydney area where mother earth is covered by very high strength sandstone and shale. It is not uncommon to see high rise building bearing on small pad footings (columns) without a need to have piles.

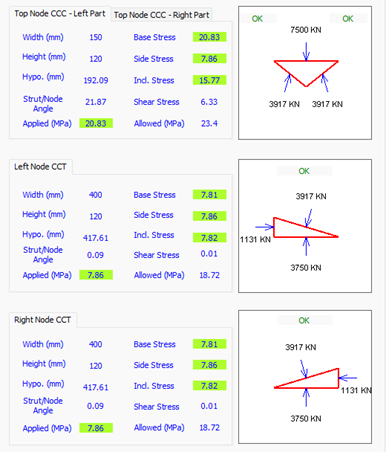
Due to the high capacity of the rock (could reach up to 12,000 KPa), the proportions of the foundation become non-flexural

The final example is addressing pad footing on rock, where the span to depth ratio is small. Look at the following figure

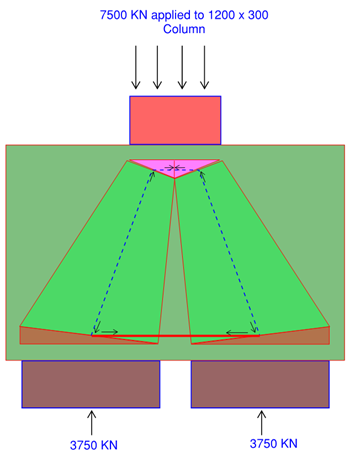
We have a factored load of 7500 KN applied onto 1000 x 1200 m² footing (depth into the page is 1200 mm), the height of the footing is 800 mm.

Inserting the numbers as in next figure will result in 2662 mm² of reo, that is N24-200 distributed over 1.2 meters. We recommend to have equal reinforcement in both directions no matter what, and a minimum -outstand from the column face at 450 mm to allow for the column reo to cog.

Participation of the confining rock can be claimed, however, it is not recommended.

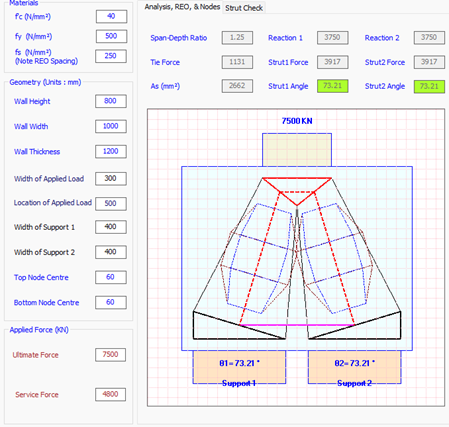
Once the reinforcement is good to go, look at the nodal stresses, and note the redundancies we have since the full width of the footing is not 100% utilised.

You should in all cases check the geotechnical pressure under the footing and make sure this one is under the allowable bearing pressure specified in the geotechnical report.

See next figure

We hope you enjoy RKALC!